Chemical/Phase Equilibria
Contents
Chemical/Phase Equilibria#
This recitation presents a solution to Assignment 04 from the Unit 02 assignment.
Topics Covered#
Unit 02 - Assignment 04 (Chemical and Phase Equilibrium; for loops)
import numpy as np
import matplotlib.pyplot as plt
import scipy.optimize as opt
Example Problem#
Problem Statement, Rawlings and Ekerdt#
Consider the gas-phase reaction
Product C has a fairly low vapor pressure, so we are concerned about the formation of a liquid phase in the reactor. The Clausius-Clapeyron equation gives the vapor pressure of component C in units of bar as a function of temperature.
The reactor is initially filled with an equimolar mixture of A and B. The equilibrium constant at T = 298K is K = 9, the reaction is exothermic with \(\Delta H^{\circ} = -11\) kcal/mol, and the system pressure is P = 1.5 bar. Components A and B are not very soluble in liquid C, so you can assume that if a liquid phase forms, it is pure species C (A and B do not condense). The heat of vaporization of component C is \(\Delta {H_{\text{vap}}} = 6\) kcal/mol, and the value of the Clausius-Clapeyron contant is c = 9.53.
Part 1#
Over what temperature range does the reactor contain a liquid phase?
Solution Part 1a:#
Calculate the equilibrium partial pressures for all species at 298K and 1.5 bar.
def obj1a(ex):
NA0 = 1.0 #mole
NB0 = 1.0 #mole
NC0 = 0.0 #moles
T = 298 #K
P = 1.5 #bar
P0 = 1.0 #bar
NA = NA0 - ex #moles
NB = NB0 - ex #moles
NC = NC0 + ex #moles
NT = NA + NB + NC
yA = NA/NT
yB = NB/NT
yC = NC/NT
aA = yA*P/P0
aB = yB*P/P0
aC = yC*P/P0
KTHERMO = 9
KACTIVITY = aC/aA/aB
OBJECTIVE = KTHERMO - KACTIVITY
return OBJECTIVE
ans, info = opt.newton(obj1a, 0.5, full_output = 'True')
#Workup
NA0 = 1.0 #mole
NB0 = 1.0 #mole
NC0 = 0.0 #moles
P = 1.5 #bar
NA = NA0 - ans #moles
NB = NB0 - ans #moles
NC = NC0 + ans #moles
NT = NA + NB + NC
yA = NA/NT
yB = NB/NT
yC = NC/NT
pA = yA*P
pB = yB*P
pC = yC*P
print(f'The pressures of A, B, and C are {pA:0.3f}, {pB:0.3f}, {pC:0.3f} in bar')
The pressures of A, B, and C are 0.312, 0.312, 0.876 in bar
Solution Part 1b#
Calculate the equilibrium partial pressures for all species at 400K and 1.5 bar.
def obj1b(ex):
NA0 = 1.0 #mole
NB0 = 1.0 #mole
NC0 = 0.0 #moles
T0 = 298 #K
T = 400 #K
P = 1.5 #bar
P0 = 1.0 #bar
DH0 = -11.0 #kcal/mol
R = 1.987e-3 #kcal/mol/K
NA = NA0 - ex #moles
NB = NB0 - ex #moles
NC = NC0 + ex #moles
NT = NA + NB + NC
yA = NA/NT
yB = NB/NT
yC = NC/NT
aA = yA*P/P0
aB = yB*P/P0
aC = yC*P/P0
K0 = 9
KTHERMO = K0*np.exp(-DH0/R*(1/T - 1/T0))
KACTIVITY = aC/aA/aB
OBJECTIVE = KTHERMO - KACTIVITY
return OBJECTIVE
And the workup:
ans, info = opt.newton(obj1b, 0.5, full_output = 'True')
#Workup
NA0 = 1.0 #mole
NB0 = 1.0 #mole
NC0 = 0.0 #moles
P = 1.5 #bar
NA = NA0 - ans #moles
NB = NB0 - ans #moles
NC = NC0 + ans #moles
NT = NA + NB + NC
yA = NA/NT
yB = NB/NT
yC = NC/NT
pA = yA*P
pB = yB*P
pC = yC*P
print(f'The pressures of A, B, and C are {pA:0.3f}, {pB:0.3f}, {pC:0.3f} in bar')
def obj1b(ex):
NA0 = 1.0 #mole
NB0 = 1.0 #mole
NC0 = 0.0 #moles
T0 = 298 #K
T = 400 #K
P = 1.5 #bar
P0 = 1.0 #bar
DH0 = -11.0 #kcal/mol
R = 1.987e-3 #kcal/mol/K
NA = NA0 - ex #moles
NB = NB0 - ex #moles
NC = NC0 + ex #moles
NT = NA + NB + NC
yA = NA/NT
yB = NB/NT
yC = NC/NT
aA = yA*P/P0
aB = yB*P/P0
aC = yC*P/P0
K0 = 9
KTHERMO = K0*np.exp(-DH0/R*(1/T - 1/T0))
KACTIVITY = aC/aA/aB
OBJECTIVE = KTHERMO - KACTIVITY
return OBJECTIVE
ans, info = opt.newton(obj1b, 0.5, full_output = 'True')
#Workup
NA0 = 1.0 #mole
NB0 = 1.0 #mole
NC0 = 0.0 #moles
P = 1.5 #bar
NA = NA0 - ans #moles
NB = NB0 - ans #moles
NC = NC0 + ans #moles
NT = NA + NB + NC
yA = NA/NT
yB = NB/NT
yC = NC/NT
pA = yA*P
pB = yB*P
pC = yC*P
print(f'The pressures of A, B, and C are {pA:0.3f}, {pB:0.3f}, {pC:0.3f} in bar')
The pressures of A, B, and C are 0.729, 0.729, 0.042 in bar
Solution Part 1c:#
Now make that general so we can easily adapt to solve for any temperature…
def temp(ex, T):
NA0 = 1.0 #mole
NB0 = 1.0 #mole
NC0 = 0.0 #moles
T0 = 298 #K
#T = 400 #K
P = 1.5 #bar
P0 = 1.0 #bar
DH0 = -11.0 #kcal/mol
R = 1.987e-3 #kcal/mol/K
NA = NA0 - ex #moles
NB = NB0 - ex #moles
NC = NC0 + ex #moles
NT = NA + NB + NC
yA = NA/NT
yB = NB/NT
yC = NC/NT
aA = yA*P/P0
aB = yB*P/P0
aC = yC*P/P0
K0 = 9
KTHERMO = K0*np.exp(-DH0/R*(1/T - 1/T0))
KACTIVITY = aC/aA/aB
OBJECTIVE = KTHERMO - KACTIVITY
return OBJECTIVE
Construct objective using lambda function; solve
Tval = 400 #K
obj1c = lambda ex: temp(ex, Tval)
ans, info = opt.newton(obj1c, 0.5, full_output = True)
def temp(ex, T):
NA0 = 1.0 #mole
NB0 = 1.0 #mole
NC0 = 0.0 #moles
T0 = 298 #K
#T = 400 #K
P = 1.5 #bar
P0 = 1.0 #bar
DH0 = -11.0 #kcal/mol
R = 1.987e-3 #kcal/mol/K
NA = NA0 - ex #moles
NB = NB0 - ex #moles
NC = NC0 + ex #moles
NT = NA + NB + NC
yA = NA/NT
yB = NB/NT
yC = NC/NT
aA = yA*P/P0
aB = yB*P/P0
aC = yC*P/P0
K0 = 9
KTHERMO = K0*np.exp(-DH0/R*(1/T - 1/T0))
KACTIVITY = aC/aA/aB
OBJECTIVE = KTHERMO - KACTIVITY
return OBJECTIVE
Tval = 400 #K
obj1c = lambda ex: temp(ex, Tval)
ans, info = opt.newton(obj1c, 0.5, full_output = True)
Solution Part 1d#
Now we’re ready to solve the actual problem. We’ll start by solving for the equilibrium partial pressure of species C for a large set of temperatures. We’ll use a for loop to run opt.newton or opt.brent many times…
Tset = np.linspace(200, 400, 100)
pCout1 = np.zeros(len(Tset))
for i in range(0, len(Tset)):
Tval = Tset[i]
obj1d = lambda ex: temp(ex, Tval)
ans, info = opt.newton(obj1d, 0.999, full_output = True)
if info.converged == False:
print('Solver failed to Converge')
break
#Workup
NA0 = 1.0 #mole
NB0 = 1.0 #mole
NC0 = 0.0 #moles
P = 1.5 #bar
NA = NA0 - ans #moles
NB = NB0 - ans #moles
NC = NC0 + ans #moles
NT = NA + NB + NC
yA = NA/NT
yB = NB/NT
yC = NC/NT
pA = yA*P
pB = yB*P
pC = yC*P
pCout1[i] = pC
Tset = np.linspace(200, 400, 100)
pCout1 = np.zeros(len(Tset))
for i in range(0, len(Tset)):
Tval = Tset[i]
obj1d = lambda ex: temp(ex, Tval)
ans, info = opt.newton(obj1d, 0.999, full_output = True)
if info.converged == False:
print('Solver failed to Converge')
break
#Workup
NA0 = 1.0 #mole
NB0 = 1.0 #mole
NC0 = 0.0 #moles
P = 1.5 #bar
NA = NA0 - ans #moles
NB = NB0 - ans #moles
NC = NC0 + ans #moles
NT = NA + NB + NC
yA = NA/NT
yB = NB/NT
yC = NC/NT
pA = yA*P
pB = yB*P
pC = yC*P
pCout1[i] = pC
plt.figure(1, figsize = (5,5))
plt.plot(Tset, pCout1, label = 'pC')
plt.ylim(0, 1.6)
plt.yticks(np.arange(0, 1.61, 0.4))
plt.xlim(Tset[0], Tset[-1])
plt.ylabel('Pressure (bar)', fontsize = 14)
plt.xlabel('Temperature (K)', fontsize = 14)
plt.legend()
plt.show()
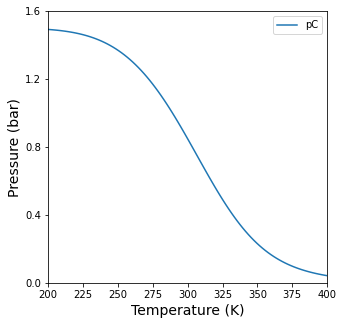
Solution Part 1e#
Now let’s compare that to the vapor pressure of species C, which we can evaluate directly from the Clausius-Clapeyron Equation.
Product C has a fairly low vapor pressure, so we are concerned about the formation of a liquid phase in the reactor. The Clausius-Clapeyron equation gives the vapor pressure of component C in units of bar as a function of temperature.
The reactor is initially filled with an equimolar mixture of A and B. The equilibrium constant at T = 298K is K = 9, the reaction is exothermic with \(\Delta H^{\circ} = -11\) kcal/mol, and the system pressure is P = 1.5 bar. Components A and B are not very soluble in liquid C, so you can assume that if a liquid phase forms, it is pure species C (A and B do not condense). The heat of vaporization of component C is \(\Delta {H_{\text{vap}}} = 6\) kcal/mol, and the value of the Clausius-Clapeyron contant is c = 9.53.
def pCsat(T):
c = 9.53
DHvap = 6 #kcal/mol
R = 1.987e-3 #kcal/mol/K
return np.exp(c - DHvap/R/T)
def pCsat(T):
c = 9.53
DHvap = 6 #kcal/mol
R = 1.987e-3 #kcal/mol/K
return np.exp(c - DHvap/R/T)
plt.figure(1, figsize = (5,5))
plt.plot(Tset, pCout1, label = 'pC')
plt.plot(Tset, pCsat(Tset), label = 'pCsat')
plt.ylim(0, 8)
plt.yticks(np.arange(0, 8.1, 1))
plt.xlim(Tset[0], Tset[-1])
plt.ylabel('Pressure (bar)', fontsize = 14)
plt.xlabel('Temperature (K)', fontsize = 14)
plt.fill_between(Tset, pCout1, pCsat(Tset), where = pCout1 >= pCsat(Tset), interpolate = True, color = 'red', alpha = 0.15, label = 'pC > pCsat: liquid present')
plt.legend(loc = 'upper left')
plt.show()
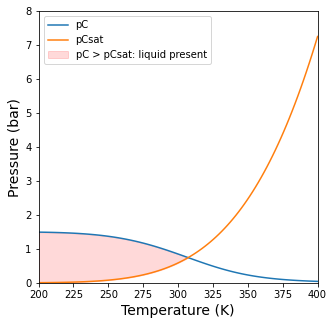
Finding the transition temperature#
If you want to solve for the exact temperature where the two curves intersect, there are many ways you can probably do it. Below, I show a modification to our objective function so that it takes two unknowns (ex and Temperature) in a vector argument (var). You’ll note that I added a second constraint equation to the equilibrium problem, which is that pC = pCsat. This will solve for the intersection temperature in the figure above (and the extent at that temperature).
def obj1e(var):
ex = var[0]
T = var[1]
NA0 = 1.0 #mole
NB0 = 1.0 #mole
NC0 = 0.0 #moles
T0 = 298 #K
#T = 400 #K
P = 1.5 #bar
P0 = 1.0 #bar
DH0 = -11.0 #kcal/mol
R = 1.987e-3 #kcal/mol/K
NA = NA0 - ex #moles
NB = NB0 - ex #moles
NC = NC0 + ex #moles
NT = NA + NB + NC
yA = NA/NT
yB = NB/NT
yC = NC/NT
PC = yC*P
aA = yA*P/P0
aB = yB*P/P0
aC = yC*P/P0
K0 = 9
KTHERMO = K0*np.exp(-DH0/R*(1/T - 1/T0))
KACTIVITY = aC/aA/aB
OBJECTIVE1 = KTHERMO - KACTIVITY
OBJECTIVE2 = PC - pCsat(T)
return [OBJECTIVE1, OBJECTIVE2]
def obj1e(var):
ex = var[0]
T = var[1]
NA0 = 1.0 #mole
NB0 = 1.0 #mole
NC0 = 0.0 #moles
T0 = 298 #K
#T = 400 #K
P = 1.5 #bar
P0 = 1.0 #bar
DH0 = -11.0 #kcal/mol
R = 1.987e-3 #kcal/mol/K
NA = NA0 - ex #moles
NB = NB0 - ex #moles
NC = NC0 + ex #moles
NT = NA + NB + NC
yA = NA/NT
yB = NB/NT
yC = NC/NT
PC = yC*P
aA = yA*P/P0
aB = yB*P/P0
aC = yC*P/P0
K0 = 9
KTHERMO = K0*np.exp(-DH0/R*(1/T - 1/T0))
KACTIVITY = aC/aA/aB
OBJECTIVE1 = KTHERMO - KACTIVITY
OBJECTIVE2 = PC - pCsat(T)
return [OBJECTIVE1, OBJECTIVE2]
opt.root(obj1e, [0.5, 300])
fjac: array([[-0.99541068, 0.09569527],
[-0.09569527, -0.99541068]])
fun: array([ 1.11639586e-10, -1.67610370e-12])
message: 'The solution converged.'
nfev: 11
qtf: array([-6.02853354e-08, -4.88374628e-09])
r: array([14.3419963 , 0.79060035, 0.09239627])
status: 1
success: True
x: array([ 0.66161408, 307.21390082])
Basically, above 307.2K, there is no liquid phase. Below 307.2K, there is a liquid phase.
Problem 2
If the reaction is endothermic with \(\Delta H^{\circ} = 11\) kcal/mol, over what temperature range does the reactor contain a liquid phase?
def temp2(ex, T):
NA0 = 1.0 #mole
NB0 = 1.0 #mole
NC0 = 0.0 #moles
T0 = 298 #K
#T = 400 #K
P = 1.5 #bar
P0 = 1.0 #bar
DH0 = 11.0 #kcal/mol
R = 1.987e-3 #kcal/mol/K
NA = NA0 - ex #moles
NB = NB0 - ex #moles
NC = NC0 + ex #moles
NT = NA + NB + NC
yA = NA/NT
yB = NB/NT
yC = NC/NT
aA = yA*P/P0
aB = yB*P/P0
aC = yC*P/P0
K0 = 9
KTHERMO = K0*np.exp(-DH0/R*(1/T - 1/T0))
KACTIVITY = aC/aA/aB
OBJECTIVE = KTHERMO - KACTIVITY
return OBJECTIVE
Tset = np.linspace(200, 400, 100)
pCout2 = np.zeros(len(Tset))
for i in range(0, len(Tset)):
Tval = Tset[i]
obj2a = lambda ex: temp2(ex, Tval)
ans, info = opt.newton(obj2a, 0.999, full_output = True)
if info.converged == False:
print('Solver failed to Converge')
break
#Workup
NA0 = 1.0 #mole
NB0 = 1.0 #mole
NC0 = 0.0 #moles
P = 1.5 #bar
NA = NA0 - ans #moles
NB = NB0 - ans #moles
NC = NC0 + ans #moles
NT = NA + NB + NC
yA = NA/NT
yB = NB/NT
yC = NC/NT
pA = yA*P
pB = yB*P
pC = yC*P
pCout2[i] = pC
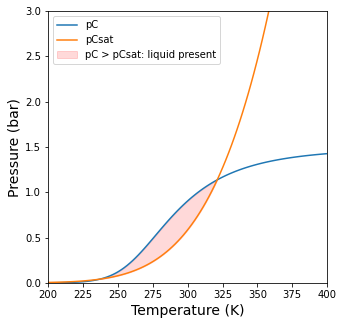
plt.figure(1, figsize = (5,5))
plt.plot(Tset, pCout2, label = 'pC')
plt.plot(Tset, pCsat(Tset), label = 'pCsat')
plt.ylim(0, 3)
plt.yticks(np.arange(0, 3.1, 0.5))
plt.xlim(Tset[0], Tset[-1])
plt.ylabel('Pressure (bar)', fontsize = 14)
plt.xlabel('Temperature (K)', fontsize = 14)
plt.fill_between(Tset, pCout2, pCsat(Tset), where = pCout2 >= pCsat(Tset), interpolate = True, color = 'red', alpha = 0.15, label = 'pC > pCsat: liquid present')
plt.legend(loc = 'upper left')
plt.show()
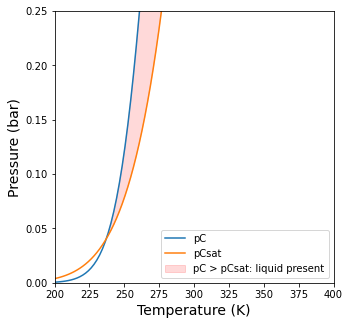
plt.figure(2, figsize = (5,5))
plt.plot(Tset, pCout2, label = 'pC')
plt.plot(Tset, pCsat(Tset), label = 'pCsat')
plt.ylim(0, 0.25)
plt.yticks(np.arange(0, 0.26, 0.05))
plt.xlim(Tset[0], Tset[-1])
plt.ylabel('Pressure (bar)', fontsize = 14)
plt.xlabel('Temperature (K)', fontsize = 14)
plt.fill_between(Tset, pCout2, pCsat(Tset), where = pCout2 >= pCsat(Tset), interpolate = True, color = 'red', alpha = 0.15, label = 'pC > pCsat: liquid present')
plt.legend(loc = 'lower right')
plt.show()
def obj2b(var):
ex = var[0]
T = var[1]
NA0 = 1.0 #mole
NB0 = 1.0 #mole
NC0 = 0.0 #moles
T0 = 298 #K
#T = 400 #K
P = 1.5 #bar
P0 = 1.0 #bar
DH0 = 11.0 #kcal/mol
R = 1.987e-3 #kcal/mol/K
NA = NA0 - ex #moles
NB = NB0 - ex #moles
NC = NC0 + ex #moles
NT = NA + NB + NC
yA = NA/NT
yB = NB/NT
yC = NC/NT
PC = yC*P
aA = yA*P/P0
aB = yB*P/P0
aC = yC*P/P0
K0 = 9
KTHERMO = K0*np.exp(-DH0/R*(1/T - 1/T0))
KACTIVITY = aC/aA/aB
OBJECTIVE1 = KTHERMO - KACTIVITY
OBJECTIVE2 = PC - pCsat(T)
return [OBJECTIVE1, OBJECTIVE2]
opt.root(obj2b, [0.2, 230])
fjac: array([[-0.92096132, 0.38965402],
[-0.38965402, -0.92096132]])
fun: array([ 6.88048230e-12, -9.28743193e-13])
message: 'The solution converged.'
nfev: 20
qtf: array([-4.78581906e-09, -1.25987421e-09])
r: array([ 2.18306257e+00, -8.58397519e-03, -1.14420384e-03])
status: 1
success: True
x: array([5.25451872e-02, 2.37072654e+02])
There is a liquid phase present between 237.1K and 321.2K. In this region, pC > pCsat, so there will be condensation.

