Material Balances XVI
Contents
Material Balances XVI#
This lecture continues with a discussion of yield, selectivity, and optimization. We also discuss instantaneous selectivity and how we can use it to inform reactor selection and ideal operating conditions.
import numpy as np
import matplotlib.pyplot as plt
import scipy.optimize as opt
from scipy.integrate import solve_ivp
from scipy.interpolate import interp1d
Looking more closely at Yield and Selectivity in flow reactors#
Rawlings, Example 4.5:
You are carrying out Benzene Pyrolysis in a Plug Flow Reactor operating at 1033K and 1.0 atm. The two reactions occurring in this system are benzene coupling to form diphenyl and hydrogen followed by a secondary reaction between benzene and diphenyl to form triphenyl and hydrogen:
Both reactions are reversible and follow elementary rate laws. Rate constants and equilibrium concentration ratios (\(K_C\)) are given below.
If pure benzene is fed into the reactor at 60,000 moles per hour, find the PFR volume required to maximize the yield to diphenyl.
def P01(V, var):
FB, FD, FH, FT = var
R = 0.08206 #L*atm/mol/K
T = 1033 #K
P = 1.0 #atm
kf1 = 7e5 #L/mol/h
kf2 = 4e5 #L/mol/h
KC1 = 0.31
KC2 = 0.48
kr1 = kf1/KC1
kr2 = kf2/KC2
FTot = FB + FD + FH + FT
Q = FTot*R*T/P
CB = FB/Q
CD = FD/Q
CH = FH/Q
CT = FT/Q
r1 = kf1*CB**2 - kr1*CD*CH
r2 = kf2*CB*CD - kr2*CT*CH
RB = -2*r1 - r2
RD = r1 - r2
RH = r1 + r2
RT = r2
dFBdV = RB
dFDdV = RD
dFHdV = RH
dFTdV = RT
return [dFBdV, dFDdV, dFHdV, dFTdV]
#This cell solves the ODE system (an initial value problem) using solve_ivp
FBf = 60000 #mol/h
FDf = 0
FHf = 0
FTf = 0
#Solve the problem
vspan = (0, 5000) #L
var0 = [FBf, FDf, FHf, FTf]
solMR01 = solve_ivp(P01, vspan, var0, atol = 1e-12, rtol = 1e-12)
#Extract data from the solution structure.
Vout = solMR01.t
FBout = solMR01.y[0]
FDout = solMR01.y[1]
FHout = solMR01.y[2]
FTout = solMR01.y[3]
#Calculate conversion
XBout = (FBf - FBout)/FBf
#Calculate diphenyl/triphenyl yield
YDB = FDout*2/FBf
YTB = FTout*3/FBf
#Calculate diphenyl selectivity
SDB = FDout*2/(FBf - FBout)
STB = FTout*3/(FBf - FBout)
#Plot yields vs. volume
plt.plot(Vout, YDB, label = 'Diphenyl Yield')
plt.plot(Vout, YTB, label = 'Triphenyl Yield')
plt.xlim(0, max(vspan))
plt.ylim(0, 1)
plt.xlabel('Volume (L)')
plt.ylabel('Yield')
plt.legend()
plt.show()
C:\Users\jqbond\AppData\Local\Temp\ipykernel_10156\3103956950.py:27: RuntimeWarning: invalid value encountered in true_divide
SDB = FDout*2/(FBf - FBout)
C:\Users\jqbond\AppData\Local\Temp\ipykernel_10156\3103956950.py:28: RuntimeWarning: invalid value encountered in true_divide
STB = FTout*3/(FBf - FBout)
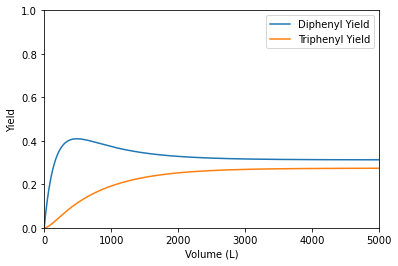
indexP = np.argmax(YDB)
print(f'The maximum diphenyl yield in a PFR is {YDB[indexP]:0.2f} at a Volume of {Vout[indexP]:0.0f}L.')
The maximum diphenyl yield in a PFR is 0.41 at a Volume of 488L.
Rawlings, Example 4.5 in a CSTR:
You are carrying out Benzene Pyrolysis in a CSTR operating at 1033K and 1.0 atm. The two reactions occurring in this system are benzene coupling to form diphenyl and hydrogen followed by a secondary reaction between benzene and diphenyl to form triphenyl and hydrogen:
Both reactions are reversible and follow elementary rate laws. Rate constants and equilibrium concentration ratios (\(K_C\)) are given below.
If pure benzene is fed into the reactor at 60,000 moles per hour, find the CSTR volume required to maximize diphenyl yield.
def P02(var, V):
#Unknowns
e1 = var[0]
e2 = var[1]
#Parameters and constants from problem statement.
T = 1033 #K
P = 1.0 #atm
R = 0.08206 #L*atm/mol/K
k1f = 7.0e5 #L/mol/h
k2f = 4.0e5 #L/mol/h
KC1 = 0.31
KC2 = 0.48
k1r = k1f/KC1 #L/mol/h
k2r = k2f/KC2 #L/mol/h
FBf = 60000 #mol/h
FDf = 0
FHf = 0
FTf = 0
FB = FBf - 2*e1 - 1*e2
FD = FDf + 1*e1 - 1*e2
FH = FHf + 1*e1 + 1*e2
FT = FTf + 0*e1 + 1*e2
FTOT = FB + FD + FH + FT
Q = FTOT*R*T/P
CB = FB/Q
CD = FD/Q
CH = FH/Q
CT = FT/Q
r1 = k1f*CB**2 - k1r*CD*CH
r2 = k2f*CB*CD - k2r*CT*CH
RB = -2*r1 - r2
RD = r1 - r2
RH = r1 + r2
RT = r2
XB = (FBf - FB)/FBf
#Constraint equations
F1 = FBf - FB + RB*V
F2 = FDf - FD + RD*V
return [F1, F2]
#Create a list of volumes we're interested in solving, we'll just go from 1 to 25000L
#We'll do this in 100 elements. Basically, we're going to have to solve the above system for 100 different volumes.
V = np.linspace(1, 5000, 100)
extent = np.zeros((len(V), 2))
for i, vol in enumerate(V):
obj02 = lambda var: P02(var, vol)
var0 = (10000, 10000)
solMR04 = opt.root(obj02, var0)
extent[i,:] = solMR04.x
extent
FB = FBf - 2*extent[:,0] - 1*extent[:,1]
FD = FDf + 1*extent[:,0] - 1*extent[:,1]
FH = FHf + 1*extent[:,0] + 1*extent[:,1]
FT = FTf + 0*extent[:,0] + 1*extent[:,1]
#Calculate conversion
XBout = (FBf - FB)/FBf
#Calculate diphenyl/triphenyl yield
YDB = FD*2/FBf
YTB = FT*3/FBf
#Calculate diphenyl selectivity
SDB = FDout*2/(FBf - FBout)
STB = FTout*3/(FBf - FBout)
C:\Users\jqbond\AppData\Local\Temp\ipykernel_10156\1502422857.py:26: RuntimeWarning: invalid value encountered in true_divide
SDB = FDout*2/(FBf - FBout)
C:\Users\jqbond\AppData\Local\Temp\ipykernel_10156\1502422857.py:27: RuntimeWarning: invalid value encountered in true_divide
STB = FTout*3/(FBf - FBout)
#Plot yields vs. volume
plt.plot(V, YDB, label = 'Diphenyl Yield')
plt.plot(V, YTB, label = 'Triphenyl Yield')
plt.xlim(0, max(V))
plt.ylim(0, 1)
plt.xlabel('Volume (L)')
plt.ylabel('Yield')
plt.legend()
plt.show()
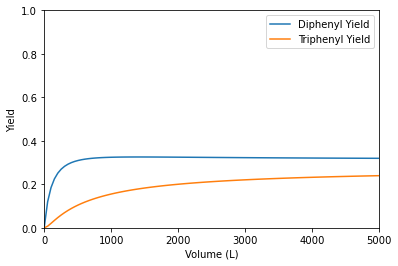
indexC = np.argmax(YDB)
print(f'The maximum diphenyl yield in a CSTR is {YDB[indexC]:0.2f} at a Volume of {V[indexC]:0.0f}L.')
The maximum diphenyl yield in a CSTR is 0.33 at a Volume of 1415L.
The main takeaway: the PFR is intrinsically more selective for diphenyl production than the CSTR. Next, we’ll learn why that is and how to make predictions about which reactors will be more selective (for parallel reactions like this one) without needing to solve material balances.
Instantaneous Selectivity#
When we start working with multiple reactions, we have to make a lot of considerations in order to maximize yield and selectivity to a desired pathway and minimize side reactions. There are a lot of ways for us to do this. Above, we considered how to operate one reactor in order to maximize yield for a series reaction. Another important decision will be the type of reactor that we use and our selection of operating conditions. Much of this can be determined by considering instantaneous selectivities for the simple case of two, irreversible parallel reactions. As reactions become more complex (series, equilibrium limited, etc.), we have to consider additional aspects of reactor operation, but the general conclusions we’ll make by considering two irreversible reactions occcuring in parallel will always hold, so these are useful insights.
Let’s start with a general definition of instantaneous selectivity. It is a quantity that is defined not based on total moles or molar flowrates, but on the rates at which specific products are formed. Specifically, we define the instantaneous selectivity as a ratio of the rate at which one species is formed or consumed to the rate at which another species is formed or consumed.
We will consider two irreversible reactions occuring in parallel. A and B can react to form a desired product, D, and an undesired product, U:
We would define the “instantaneous selectivity of D with respect to U” as the rate at which D is formed divided by the rate at which U is formed:
Note that “instantaneous selectivity” is just a general concept comprising a ratio of production rates. You could define similar ratios between any two species of interest, e.g., D with respect to A:
U with respect to B:
B with respect to A:
Or A with respect to both U and D:
We can define an instantaneous selectivity for any ratio of rates that are important in our system. Here, we only have two parallel reactions, and we’re only making U and D, so the most informative instantaneous selectivity to consider is the rate at which D forms relative to the rate at which U forms. Ideally, we’d like to maximize that quantity:
Now we have to express production rates in terms of reaction rates.
Here, we have two reactions, and we’ll say, generally, that their rates are given by a general expression:
The reaction orders are as yet unspecified, and we’ll state explicitly that \(k_1\) and \(k_2\) are both functions of temperature, and their dependency is given by an Arrhenius expression so that:
With that in mind, the instantaneous selectivity expression of interest becomes:
And we again note that both rate constants are implicit functions of temperature given by an Arrhenius expression.
We can also express that quantity as follows, which highlights that differences in reaction orders and rate constants are important in determining instantaneous selectivities.
We can’t make any further decisions until we know more about the reaction orders and rate constants, so now we’ll specify cases we’d like to consider.
Case 1: \(k_1 = k_2\), \(\alpha_1 > \alpha_2\), \(\beta_1 > \beta_2\)
For this scenario, we conclude that:
\((\alpha_1 - \alpha_2) = a\), and a is positive
\((\beta_1 - \beta_2) = b\), and b is positive
rate constants cancel from the instantaneous selectivity expression
This gives:
Where both \(a\) and \(b\) are positive. We consider limiting behavior:
As \(C_A, C_B \longrightarrow 0\), \(\tilde{S}_{D/U} \longrightarrow 0\)
As \(C_A, C_B \longrightarrow \infty\), \(\tilde{S}_{D/U} \longrightarrow \infty\)
In this case, we can see that we favor selectivity to the desired product by operating at maximum concentrations of A and B. For this reason, we want to chose a reactor that allows us to operate at maximum concentrations of reacting species for as long as possible, and we want to operate that reactor such that we maintain concentrations as high as possible.
Reactor Selection: Consider a PFR or a Batch Reactor; CSTR is a poor choice for selectivity.
Operating conditions: Gas Phase (high pressure, no diluent); liquid phase (high concentration; no solvent)
Caveats: Safety, pumping, miscibility, etc.
Case 2: \(k_1 = k_2\), \(\alpha_1 < \alpha_2\), \(\beta_1 < \beta_2\)
For this scenario, we conclude that:
\((\alpha_1 - \alpha_2) = -a\), (a is positive)
\((\beta_1 - \beta_2) = -b\), (b is positive)
rate constants cancel from the instantaneous selectivity expression
This gives:
Where both \(a\) and \(b\) are positive. We rearrange this as follows, which shows the dependency more clearly:
We consider limiting behavior:
As \(C_A, C_B \longrightarrow 0\), \(\tilde{S}_{D/U} \longrightarrow \infty\)
As \(C_A, C_B \longrightarrow \infty\), \(\tilde{S}_{D/U} \longrightarrow 0\)
In this case, we can see that we favor selectivity to the desired product by operating at minimum concentrations of A and B. For this reason, we want to chose a reactor that allows us to operate at minimum concentrations of reacting species for as long as possible, and we want to operate that reactor such that we maintain concentrations as low as possible.
Reactor Selection: Consider a CSTR; PFRs and Batch reactors go from high concentration to low concentration and will be worse for selectivity.
Operating conditions: Gas Phase (low pressure, add diluent N2 or other inert); liquid phase (low concentration in a solvent)
Caveats: As concentrations go to zero, rates also go to zero, and reactor volume goes to infinity.
Case 3: \(k_1 = k_2\), \(\alpha_1 > \alpha_2\), \(\beta_1 < \beta_2\)
For this scenario, we conclude that:
\((\alpha_1 - \alpha_2) = a\), (a is positive)
\((\beta_1 - \beta_2) = -b\), (b is positive)
rate constants cancel from the instantaneous selectivity expression
This gives:
Where both \(a\) and \(b\) are positive. We rearrange this as follows, which shows the dependency more clearly:
In this case, we see that we essentially want as high a concentration of A as possible and as low a concentration of B as possible. Here, conventional CSTR, PFR, or Batch reactors don’t make much sense. We can operate this way, but we would end up having very low conversion of A per pass (since B would be so dilute), that we’d end up with a large amount of recycle and inefficient operation. So we would probably achieve high selectivity to D, but the reactor configuration would be too expensive to be practical. Here is where you may see some less conventional reactor designs:
Semi-batch reactor for liquids: Fill with A initially; add B at low flowrate.
Membrane reactor for gases: Flow A at high pressure through inner channel, diffuse B across membrane into reactor.
Case 4: \(k_1 = k_2\), \(\alpha_1 < \alpha_2\), \(\beta_1 > \beta_2\)
For this scenario, we conclude that:
\((\alpha_1 - \alpha_2) = -a\), (a is positive)
\((\beta_1 - \beta_2) = b\), (b is positive)
rate constants cancel from the instantaneous selectivity expression
This gives:
Where both \(a\) and \(b\) are positive. We rearrange this as follows, which shows the dependency more clearly:
This is the mirror image of Case 3. We would make similar conclusions.
Semi-batch reactor for liquids: Fill with B initially; add A at low flowrate.
Membrane reactor for gases: Flow B at high pressure through inner channel, diffuse A across membrane into reactor.
Case 5: \(k_1 \neq k_2\), \(\alpha_1 = \alpha_2\), \(\beta_1 = \beta_2\)
For this scenario, we conclude that:
\((\alpha_1 - \alpha_2) = 0\)
\((\beta_1 - \beta_2) = 0\)
rate constants remain in the instantaneous selectivity expression
This gives:
To go further, we have to express the rate constants in terms of their Arrhenius parameters:
Which we can also express as:
We can see that the critical operating parameter here is the treaction temperature–we don’t have much control over anything else. In general, pre-exponential factors (\(A_1\) and \(A_2\)) and barriers (\(E_{A1}\) and \(E_{A2}\)) are weak functions of temperature, so we can consider them to be constant as we vary the reaction temperature. So, the ratio of pre-exponentials never really changes as we vary temperature. For simplicity, we’ll say it is fixed:
Then:
So, the impact of temperature on instantaneous selectivity is determined by the difference in barriers for the two processes. We’ll consider a few sub-cases:
Case 5a: \(E_{A1} = E_{A2}\)
If the two barriers are equal, we find that our selectivity expression becomes:
Here, we can change temperature all we want to, and the rates of each reaction will increase and decrease in exactly the same way, so instantaneous selectivity is indpenedent of temperature.
Case 5b: \(E_{A1} > E_{A2}\)
Then, we find that \((E_{A1} - E_{A2}) = E\), where E is a positive number. So:
Examining limiting behavior, we find:
As \(T \longrightarrow 0\), \(\tilde{S}_{D/U} \longrightarrow 0\)
As \(T \longrightarrow \infty\), \(\tilde{S}_{D/U} \longrightarrow A\)
We want to operate at the highest temperature possible to maximize selectivity toward the desired product
Temperature favors the higher barrier process.
Caveat: cost of heating; as temperature gets too high, we usually “turn on” more side reactions, so approach with caution.
Case 5c: \(E_{A1} < E_{A2}\)
Then, we find that \((E_{A1} - E_{A2}) = -E\), where E is a positive number. So:
Examining limiting behavior, we find:
As \(T \longrightarrow 0\), \(\tilde{S}_{D/U} \longrightarrow \infty\)
As \(T \longrightarrow \infty\), \(\tilde{S}_{D/U} \longrightarrow A\)
We want to operate at the lowest temperature possible to maximize selectivity toward the desired product
Temperature favors the higher barrier process.
Caveat: as Temperature goes to zero, so does reaction rate, so there are practical limits to this strategy.

